확률분포는 확률변수에 따라 확률이 어떻게 흩어져 있는지를 표현함.
이 흩어져 있는 것을 표현하기 위해 함수를 도입하는 것
확률분포는 함수인 것이다.
동전을 3개 던진다고 하자.
이 때, 앞면이 나오는 횟수를 X라고 하면, 다음과 같은 결과를 얻는다.
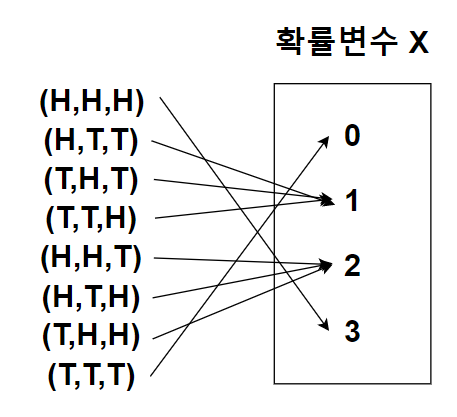
확률변수X에 관한 함수를 만들자. 각 확률변수에 대응하는 확률은 다음과 같다.
$ P(X=0)=\frac{1}{8} $
$ P(X=1)=\frac{3}{8} $
$ P(X=2)=\frac{3}{8} $
$ P(X=3)=\frac{1}{8} $
동전을 3개 던질때 앞면이 나오는 확률 f(x)는 다음과 같다.
$ f(x)=\binom{3}{x} \times (\frac {1}{2})^{x} \times (\frac {1}{2})^{3-x} = \binom {3}{x} \times \frac {1}{8}$
이 함수 $f(x)$를 이산확률변수의 확률질량함수(probability mass function)이라고 한다.
이산확률변수 X가 취할 수 있는 값 $x_{1},x_{2},...x_{n}$의 각각에 대해
확률 $P(X=x_{1}),P(X=x_{2}),...,P(X=x_{n})$를 대응시켜주는 관계를
X의 '확률질량함수'라 하고, $f(x)=P(x_{i}), x=0,1,2,...,i$로 표시한다.
확률질량함수의 성질
1. 모든 $x$에 대하여 $f(x) \geq 0 $
2. $ \sum_{i=1}^\infty f(x_{i})=1 $
3. $ P(a \leq X \leq b)=\sum_{a \leq x_{i} \leq b} f(x_{i}) $
https://blog.naver.com/mykepzzang/220835372463
[확률과 통계] 16. 확률질량함수, Probability Mass Function of Discrete Random Variable
'확률질량함수' 이름이 좀 어렵게 느껴집니다. 어쨌든 확률과 관련된 함수라는 것을 염두해 두시고..... 이...
blog.naver.com
'기초통계' 카테고리의 다른 글
| 주변확률분포와 기댓값, 분산, 공분산, 상관계수 (0) | 2019.12.16 |
|---|---|
| 이산확률변수의 결합확률분포 (0) | 2019.12.12 |
| 확률(Probability) vs 가능도(Likelihood) (0) | 2019.12.12 |
| 최대 우도 추정법(MLE) 예시 (0) | 2019.12.12 |
| MLE(Maximum Likelihood Estimation)와 MAP(Maximum A Posterior) (0) | 2019.12.11 |