머신러닝에서는 supervised learning에는 두가지의 카테고리가 있다.
Classification과 Regression임.
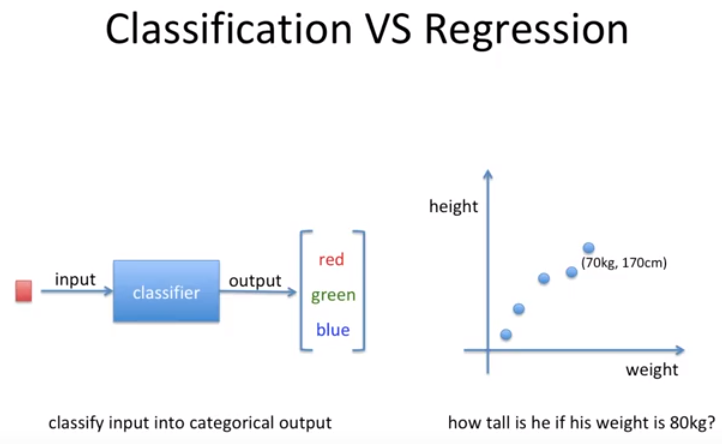
리니어 → 직선
$ y=ax+b $와 같은 1차 함수 선을 그리게 된다.
그 선을 바탕으로 예측하는 것이 회귀이다.

어떠한 선이 더 예측을 잘 할까?
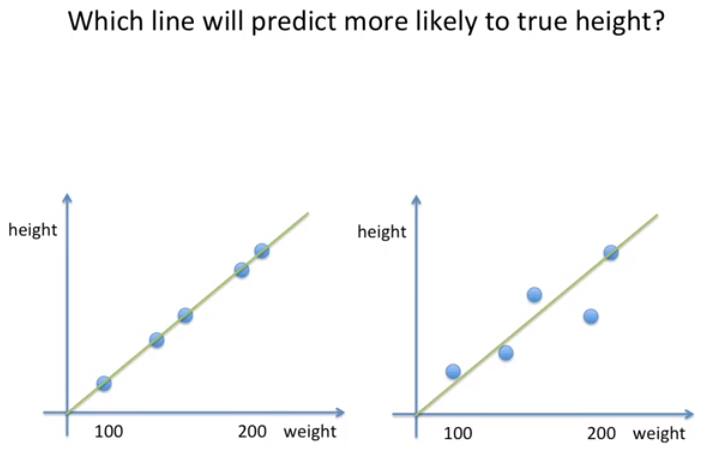
대부분의 사람들이 왼쪽이 더 잘한다고 말한다.

수치적으로 에러를 나타낼수있는데,
왼쪽에서는 에러가 전혀없고
오른쪽은 에러가 있다.
스퀘어 에러라는 개념으로 오류를 정량화할 수 있다.
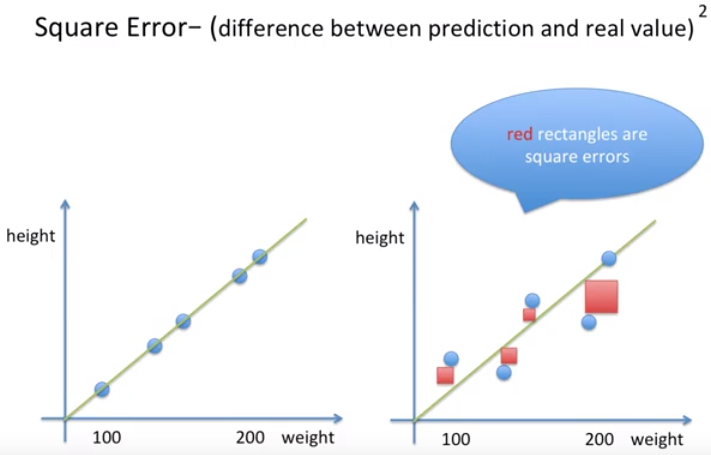
에러를 제곱한 값이다.
거리가 아니고 넓이로보자. 3가지 이유는 다음과 같다.
- 넓이로 보는 이유 → 우리는 눈에 보이기 쉽다
- 수학적으로 볼때 에러가 조금이라도 있어도 증폭시킬수있어 큰것과 작은것 비교쉽게
- 그래디언트 디센트에서 제곱이라는 개념이있으면 쉬워진다.

왼쪽이 실제값과 가깝게 예측함
이 말은 확률이라는 말이 아니다.
선형 회귀 같은 경우는 maximum likelihood 라는 말을 쓴다.
최대 발생할 가능성이 높은 쪽으로 선을 그리는게 선형 회귀이다.
관찰된 값 중에 가장 적합한 선을 그어라.
선형 회귀를 코딩하라면 어떻게 코딩할까?
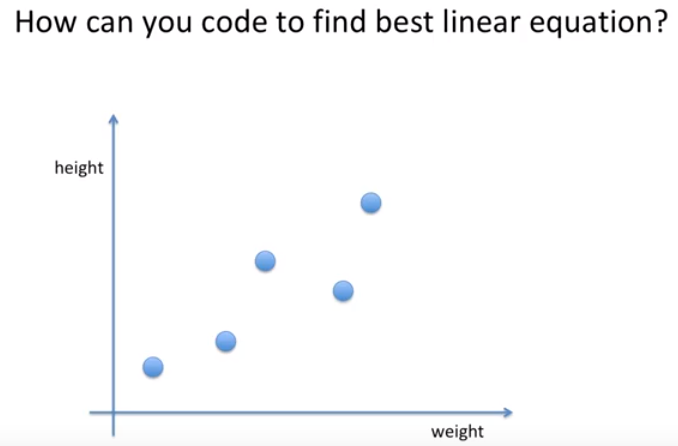
Least Mean Square(LMS) 개념을 사용할 것
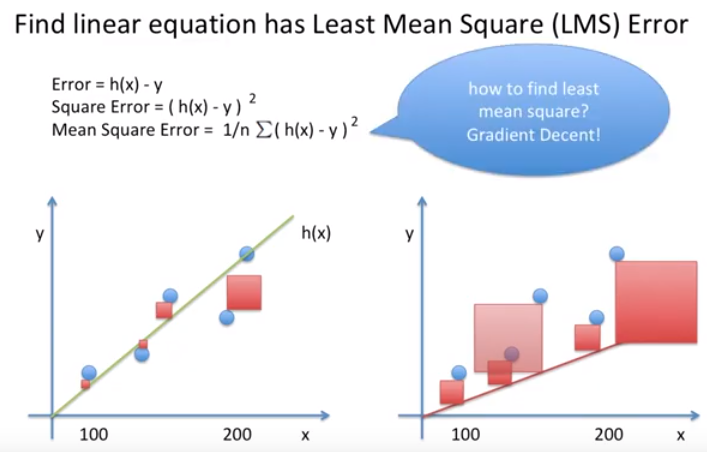
에러는 가설과 실제 있는 점과의 거리이다.
$ error = h(x) - y $
Square Error는 Error를 제곱한 값이다.
Mean Square Error는 Square Error를 평균낸 값이다.
이 값들을 사용해서 직선을 긋는다.
어떻게 베스트? 그라디언트 디센트 개념을 사용해서 한다.
코스트 펑션 -> MSE 이다.
비용함수 실제값과 가설간의 차이를 cost function이라고 한다.
이 코스트 펑션을 가장 최저로 만드는 것이 목표이고.
목표함수 object function이라고함.

머신 러닝에서는 파라미터를 세타로 표현
가장 알맞는 세타를 찾는것이다.
알파 -> 러닝레이트

learning rate = 0.01
세타 = 1
https://www.youtube.com/watch?v=MwadQ74iE-k
'머신러닝과 딥러닝' 카테고리의 다른 글
| Doc2Vec 공간의 이해 (0) | 2019.12.29 |
|---|---|
| 행렬식의 의미 (0) | 2019.12.23 |
| 고유벡터와 고유값 (0) | 2019.12.23 |
| Batch Normalization이 적용될 경우 학습속도가 개선이 되는 이유 (0) | 2019.12.19 |
| 주성분 분석(PCA) (0) | 2019.12.16 |