머신러닝 차원을 줄이고 싶을때
차원 축소는 언제 사용할까?
시각화 - 5차원 ~ 100차원
3차원 이하의 데이터로 만들어주고 차트로 보여줄수있고 데이터를 이해하기 쉬움
시각화에 PCA 알고리즘 많이 사용됨
이미지에 노이즈 감소시킬때 사용
적은 차원 공간에 저장하게 되므로써, 메모리를 절약하게 되고
용량이 작으니까 퍼포먼스도 좋아짐.
PCA는 어떻게 동작할까?

좌표상의 2차원 데이터를 어떻게 1차원으로 줄일 수 있을까?

x1축으로 내렸을때
몇개의 점은 겹치게 된다. 정보의 유실이 생긴다. 즉, 그닥 좋은 방법은아니다..

유실을 막는 좋은 방법은 무엇일까?
분산이 넓은 지역을 찾는것이다.
하나의 축에다가 점들을 놓게되는 것이다. 퍼져있는 정도를 지켜줌으로써 점들이 겹치지 않고
하나의 공간에 모이게 된다.

2차원이 1차원이 된다.
이것이 PCA 알고리즘.

축이 바로 Principal Component이다. 즉, PC
축을 어떻게 그었냐면, 이 점들이 가장 잘 퍼져있는 정도를 계산해서 살릴 수 있는 방향으로 선을 그은 것이다.
이 방향이 다른축 $x_{1}, x_{2}$로 모았을때보다 거리가 긴 것을 확인 할 수 있다.
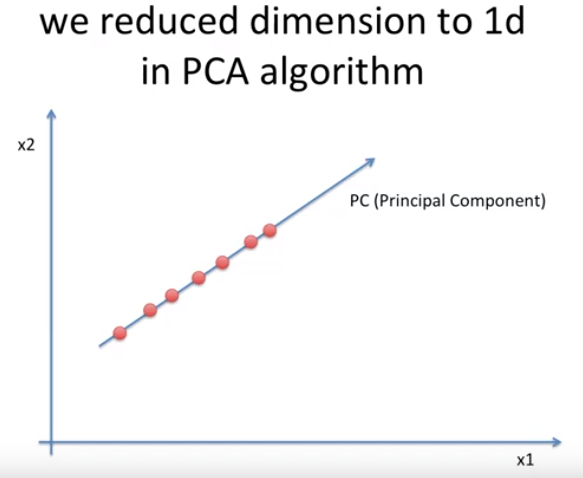
PC는 수학적으로 접근 했을 때, 이 점들이 가지고 있는 Covariance Matrix에서 Eigen Vector이다.

Eigen Vector는 2차원에서는 2개, 4차원에서는 4개 300차원에서는 300개를 갖는다.
즉, 2차원 공간에서는 두개가 있다 위와 같이.
어떠한 Eigen Vector를 선택해야 할까?
점들이 가장 넓게 퍼져 있는 Eigen Vector를 잡아야한다.
Eigen Value가 높으면 분산이 퍼져있는 정도가 높다는 뜻이다.
Covariance Matrix에서 Eigen Value의 값이 가장 높은 녀석의 Eigen Vector값을 기준으로 점들을 옮겨주면 PCA가 완료가 된다.
PCA 기반 차원 감소의 문제점
PCA의 경우 선형 분석 방식으로 값을 사상하기 때문에 차원이 감소되면서 군집화 되어 있는 데이터들이 뭉게져서 제대로 구별할 수 없는 문제를 가지고 있다. 아래 그림을 보자
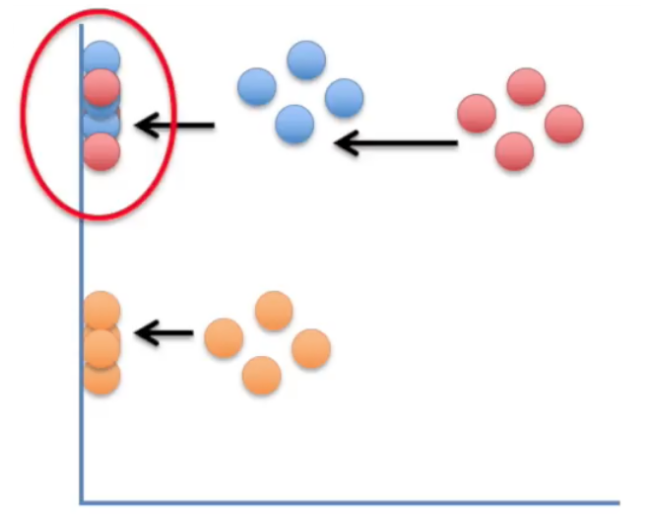
이 그림은 2차원에서 1차원으로 PCA 분석을 이용하여 차원을 줄인 예인데, 2차원에서는 파란색과 붉은색이 구별이 되는데, 1차원으로 줄면서 1차원상의 위치가 유사한 바람에, 두 군집의 변별력이 없어져 버렸다.
'머신러닝과 딥러닝' 카테고리의 다른 글
| Doc2Vec 공간의 이해 (0) | 2019.12.29 |
|---|---|
| 행렬식의 의미 (0) | 2019.12.23 |
| 고유벡터와 고유값 (0) | 2019.12.23 |
| Batch Normalization이 적용될 경우 학습속도가 개선이 되는 이유 (0) | 2019.12.19 |
| 선형회귀 (linear Regression) 이해하기 (0) | 2019.12.11 |