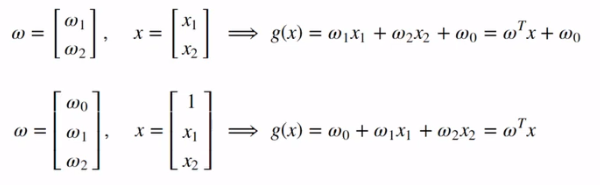
$ \omega $와 $x$가 위와 같을 때 $ g(x) $가 위와 같이 표현된다.
직선 $ g(x) = 0$과 Sign(부호)과의 관계는 다음과 같다.
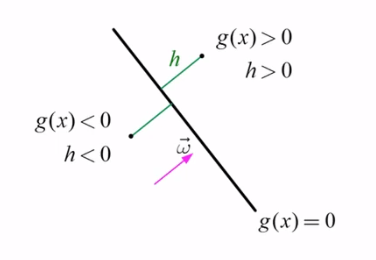
$h$가 양수이면 $g(x)$도 양수이다.
$sign(g(x))$ 에 따라서 +1, -1이 나오므로... binary classification을 하는 것이다.
linearly seperable data인 경우,
모든 데이터에 대해서 $sign(g(x))$가 성립하는
$g(x)$를 찾는 것이 문제이다.
$ \omega $를 바꿔가는 과정이 학습이고
$ g(x) = 0 $를 찾는 것이 linear classifier를 찾는것이다.
찾는 방법 중에 하나가 perceptron 알고리즘 인 것이다.
$ \omega $를 어떻게 찾는가?

클래스 1 (y=1)에 속한 모든 데이터는 $g(x) > 0$이다.
클래스 0 (y=-1)에 속한 모든 데이터는 $g(x) < 0$이다.

g(x)를 찾는 것은 $ \omega $를 찾는 것과 같은 말이다.
퍼셉트론 알고리즘

$ \omega ^Tx $를 계산하고 $sign$함수를 취한다.
N개의 training set이 주어 졌을때, $ y_{i} $는 binary기 때문에 -1(class 0)과 1(class 1)을 가진다.
$ \omega $는 랜덤하게 초기화(초기화 하는 방법은 다양함)
잘못 분류된 경우($ sign(w^Tx_{n}) \neq y_{n} $)에 가중치 업데이트를 한다.
그 점에서의 클래스($ y_{n} $)와 $x_{n}$값을 사용해서 $ \omega $를 업데이트 한다.
오분류 예시) 실제 클래스가 $y=+1$인 경우

$ w^Tx_{n} < 0 $ 였을 때, 실제 클래스가 $ y_{n} = +1 $ 이 었을 경우라면...
misclassified 된 것이다.
현재 위치는 $ \vec {x} $의 빨간점에 데이터가 있다.
$ \omega $에 수직인 직선 $ \textcolor {red} {g(x) = 0} $보다 밑에 있다. ( $ \omega $ 벡터의 반대 방향에 있다. )
실제 클래스는 1이다. (오류)
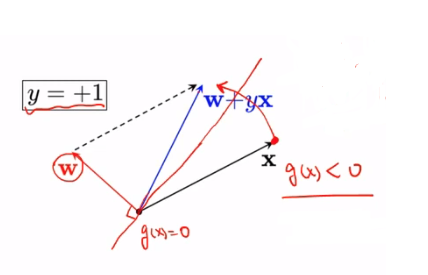
$ w \leftarrow w + y_{n}x_{n}$을 사용한다.
실제 $ y_{n} $의 값은 +1이 었으므로 그대로 대입
$ \textcolor {blue} {\omega ^{'} } \leftarrow w + (+1)x_{n}$

새로운 $ \omega ^ {'} $ 가 결정되면,
새로운 $ g'(x) = 0 $은 위와 같다.
지금의 $x$는 $w+yx$과 같은 방향에 있다. $ g'(x) > 0 $에 해당
$y$가 +1인 것과 동일해진다.
오분류 예시) 실제 클래스가 $y=-1$인 경우
$ w^Tx > 0 $인 경우 실제 클래스는 $ y=-1$ 이라면...
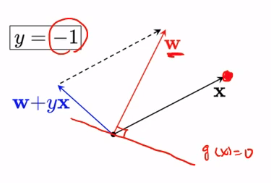
$ \textcolor {red} {x} $는 $ \omega $와 같은 방향에 있다.
실제 클래스는 $ y=-1$이었으므로 다음과 같이 업데이트를 할 수 있다.
$ \textcolor {blue} {\omega ^{'} } \leftarrow w + (-1)x_{n}$
$ x_{n} $ 에 $-1$을 곱해서 방향이 반대인 벡터를
$ \omega $와 더하면 새로운 $ \omega^{'}$이 생긴다.

$ \omega^{'}$에 수직인 새로운 직선 $ \textcolor {blue} {g'(x)=0} $이 있다.
$ \textcolor {red} {x} $는 $ \textcolor {blue} {g'(x)=0} $의 아래쪽에 있다($y=-1$)
클래스가 제대로 나눠져있으면 아무것도 하지 않는다.
오분류가 생기면 $ \omega$를 업데이트한다.
'머신러닝과 딥러닝' 카테고리의 다른 글
| 콘볼루션의 정의와 예시 (0) | 2020.01.06 |
|---|---|
| 퍼셉트론(Perceptron)은 왜 동작을 하는가? (0) | 2020.01.06 |
| 퍼셉트론(Perceptron) (2) (0) | 2020.01.04 |
| 퍼셉트론(Perceptron) (1) (0) | 2020.01.04 |
| 로지스틱 리그레션(Logistic Regression) (0) | 2020.01.02 |