2차원에서 $ \omega $의 의미가 무엇인가?
bias를 $ w_{0} $로 표현을 했음.
$ \omega $ 는 parameter이고
$ x $는 data이다.
기하학적으로
$ g(x) = w_{1}x_{1} + w_{2}x_{2} + w_{0} $로 표현할 수 있다.
$g(x)$가 양수이면 +1
$g(x)$가 음수이면 -1
이것을 결정하는 것은
$g(x) = 0$ 에 해당하는 것이 아래의 그림에서 검은색 직선이다.
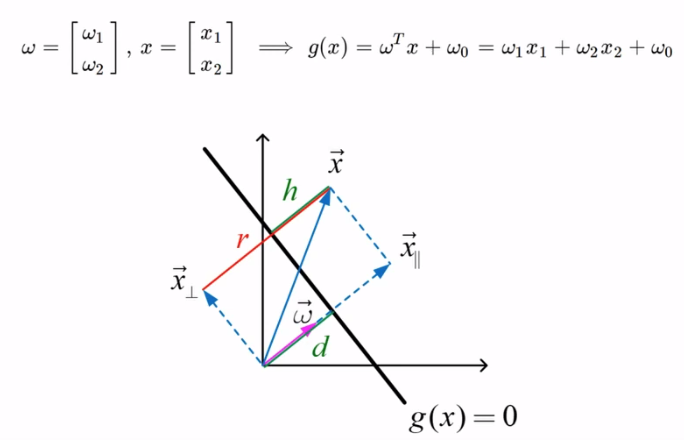
$ w_{1}x_{1} + w_{2}x_{2} + w_{0} = 0 $을 직선의 방정식으로 바꾸면 다음과 같다.
$ x_{2} = - \frac { w_{1} }{ w_{2} } x_{1} - \frac {w_{0}}{ w_{2}}$
$ - \frac {w_{1}}{w_{2}} $는 기울기에 해당하는 것이고, $ \frac {w_{0}}{w_{2}} $는 절편에 해당하는 것이다.
이것을 이제는 $ w^Tx + w_{0} $ 의 형태로 살펴보자.
$ \omega $는 열 벡터기 때문에 어떤 값을 갖는다.
$ \omega \perp g(x) = 0$ 라는 것은 $ \omega $와 $g(x)$가 수직이라는 의미이다.
$ \vec {p}$ 와 $\vec {q} $가 decision line상에 있는 두개의 점이라고 가정해보자.

$ \vec {p}$ 와 $\vec {q} $가 벡터이면서 직선($g(x)$) 상에 있기 때문에
$ g(x) = w^Tx + w_{0} $ 이므로,
$ g(\vec{p})=g(\vec{q})=w_{0}+w^T\vec{p}=w_{0}+w^T\vec{q} = 0 $이다.
이를 정리하면 다음과 같다.
$w^T(\vec {p} - \vec {q}) = 0$ 이다.
$\vec {p} - \vec {q}$는 무엇일까?? 직선 상에 있는 벡터이다.

즉, $ \omega $는 직선에 항상 수직한다!
$ \omega $를 알게 되면 $ g(x) $의 방향을 알 수 있는 것이다.
$g(x)$의 방향 정보가 $ \omega $에 들어 있는 것이다.
여러가지 직선 중에 $w_{0}$로 결정하는 것이다. (직선의 위치)
2차원에서 $ w_{0} $의 의미가 무엇인가?

$ \omega $가 주어지면 직선의 방향이 결정되는데...직선의 위치는 아직 결정되지 않았다.
원점에서 $ g(x) $까지의 거리를 d라 하자.
d를 결정하면, 여러개의 직선 중에 하나를 결정할 수 있다.
$ \textcolor {red} {x} $를 직선 상에 있고,
방향은 $ \omega $와 같고,
노말라이즈 하고 d만큼 떨어져있는 $ \textcolor {red} {x} $ 를 정의 하면 다음과같다.
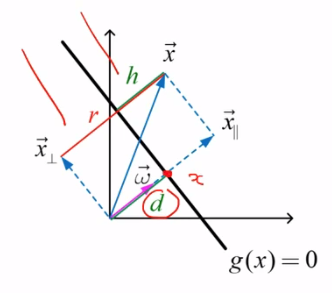
$ \textcolor {red} { \vec {x} = d \frac {\vec{w}}{ \parallel \vec {w} \parallel } }$ d는 원점에서 직선까지의 수직한 거리를 d라 하자. d는 스칼라이다.
$ \textcolor {red} { \vec {x} }$는 $ \omega $벡터와 방향성이 같다.
$ \omega $의 크기로 나누어서 유닛 벡터로 노말라이즈 했다.
$ \textcolor {red} { \vec {x} } $는 직선상에 있으니 $g(x)$에 넣어도 0이 된다.
$ g(x) = w_{0} + w^{T}x = 0 $
$ w_{0} + w^Td \frac {w} { \parallel w \parallel } = w_{0} + d \frac { w^Tw} {\parallel w \parallel} = w_{0} + d \parallel w \parallel = 0 $
$ w^{T}w $는 자기 자신을 곱한 것이므로 $ \parallel \omega \parallel^{2} $과 같다.
따라서,
$ d = - \frac {w_{0}}{\parallel w \parallel} $
$ w_{0} $가 주어지면 원점에서의 거리가 d로 결정이 된다.
d는 부호를 가지는 거리이다.
임의의 점에서
지금까지는 직선 상에 있는 두 점에 대해 말했으나,
임의의 점을 생각해보자

$ \vec {x} $를 decomposition을 시키면 다음과 같다.
$ \vec {x_\perp}$와 $ \vec {x} $와의 거리를 $r$라 하자.
임의의 $ \vec {x} $와 $g(x) $와의 거리를 $h$라 하자.
$ d+ h = r $이다.
$ \vec {x} = x_{\perp} + r \frac {w} {\parallel w \parallel} $
여기에 $ w^{T} $를 한번 곱해보면 다음과 같다.
$ w^{T}x = w^{T}(x_{\perp}+ r \frac {w} {\parallel w \parallel} ) = r \frac {w^{T}w} {\parallel w \parallel} = r \parallel w \parallel $이다.
$ w^{T}x_{\perp} $는 수직이므로 0이다.
즉, $ w^{T}x = r \parallel w \parallel $이다.
$ g(x) = w_{0} + w^Tx $에 대입하면 다음과 같다.
$ g(x) = w_{0} + r \parallel w \parallel $ 이나, $ r = d+h $ 이므로,
$ g(x) = w_{0} + (d+h) \parallel w \parallel $ 이나, $ d = - \frac {w_{0}} { \parallel w \parallel } $ 이므로,
$ g(x) = w_{0} + ( - \frac {w_{0}} { \parallel w \parallel } + h ) \parallel w \parallel $ 이다.
$ g(x) = h \parallel w \parallel $ 이다.
그러면....
$ h = \frac {g(x)} { \parallel w \parallel } $이다.
임의의 $x$가 들어갔을 때,
$ g(x) = w^{T}x + w_{0} $ 에서 $ \omega $의 $norm$으로 노말라이징 해주면 $h$가 된다.
$ g(x)$을 $ \parallel w \parallel $ 로 나누어 줬을 때 나오는 $h$가 의미하는 바는 무엇이냐 하면...
임의의 점과
직선 $ g(x) $에 수직한 거리(최단거리)를 의미한다.
$h$가 양수다 = $g(x) > 0$이다.
$h$가 음수다 = $g(x) < 0$이다.
$h$는 직선($g(x) = 0$ )으로부터 (부호가 있는) 수직한 거리이다.
'머신러닝과 딥러닝' 카테고리의 다른 글
| 퍼셉트론(Perceptron)은 왜 동작을 하는가? (0) | 2020.01.06 |
|---|---|
| 퍼셉트론(Perceptron) (3) (0) | 2020.01.06 |
| 퍼셉트론(Perceptron) (1) (0) | 2020.01.04 |
| 로지스틱 리그레션(Logistic Regression) (0) | 2020.01.02 |
| 최소자승법과 직교투영 (0) | 2019.12.31 |