$x$ 값들은 주어진 데이터
$ x_{1}, x_{2}, x_{3}, \, ... \, x_{d} $
$ \omega $로 이루어진 선형결합이라 생각하면(가정하면)
직업의 가중치가 10 ($ w_{1} $)
성별의 가중치가 1 ($ w_{2} $)
수입의 가중치가 9 ($ w_{3} $)
몸무게 가중치가 0 ($ w_{4} $)
키 가중치가 0 ($ w_{5} $)
$ f=w_{1}x_{1}+w_{2}x_{2}+ \, ... \, + w_{d}x_{d}$
$ Approve\,credit \quad if \sum_{i=1}^{d} w_{i}x_{i} > threshold $
$ Deny\,credit \quad if \sum_{i=1}^{d} w_{i}x_{i} < threshold $
중요한 팩터들이 무엇인지...
정말 관심있는 것은 weight($\omega$)값이다.
다양한 팩터를 같은 contribution(weight)으로 생각하지않을것
$ \omega$ 값이 0이면 중요한 팩터가 아닐 것이다.
Sign함수의 모양
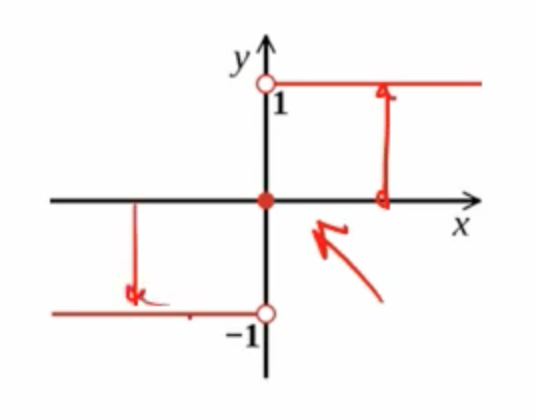

$ threshold = w_{0} * 1 $로 볼 수 있고, $ x_{0} =1$로 보면 다음과 같이 생각할 수 있다.
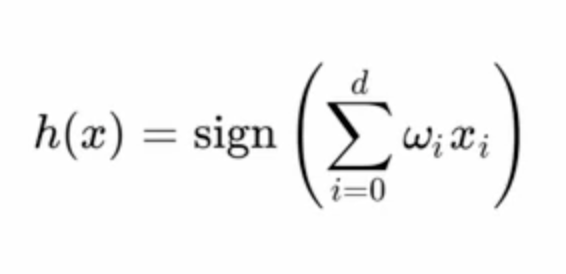
sign 함수를 넣고 음수면 -1 양수면 1로...
우리가 estimation해야하는 것은 $ \omega$이고,
$ \omega $ 해당하는 것은 classification boundary이다.
$ h(x) $는 non-linear function이다. 괄호 내부는 선형결합이지만, 외부는 sign함수로 덮여있으므로!
$x$도 $\omega$도 column 벡터이기 때문에
vector 형태로 퍼셉트론을 표현하면 다음과 같다.
$ h(x) = sign(\sum_{i=0}^{d} w_{i}x_{i}) = sign(\omega^{T} x) $
내적(inner product)의 결과는 하나의 숫자로 나오기 때문에,
양수인지 음수인지에 따라 그 값이 1 또는 -1이 나온다.
원하는 최종값이 바이너리가 되는것이다.
데이터가 주어졌을 때, $ \omega $를 찾는법
시작은 linearly seperable data(이진 분류 일때 선형 직선으로 나눌 수 있는 데이터)로 설명.
데이터 셋이 선형적으로 분류가 될 때를 가정하고 차원수를 증가시키면 다음과 같다.
2차원 공간에서는 boundary가 직선일테고,
3차원 공간에서는 평면(plane)이 될것
d차원 공간에서는 d공간 상에서의 평면, 평면의 차원은 d-1차원, 일반적으로 hyper plane이라고 이야기한다.
Hyperplane
Hyperplane의 차원은 d-1이고, D-dimensional 공간을 반으로 분리 할 수 있다.
$ \omega $를 정의하는 것이 Hyperplane이 된다.
$ \omega $는 Hyperplane 위에 있는 어떠한 벡터와도 수직이다.
그 말은
$ w^{T}x=0$이라는 의미이다.
$ w^{T}x=0=w_{0}x_{0}+w_{1}x_{1}+\,...\,+w_{d}x_{d}=0$
D 공간 상에서 d개가 있고,
위 조건을 만족하는 점들의 집합($x_{1}, x_{2},\, ,,, \, x_{d} $은 hyperplane 상에 있을 것
(이진 분류)
d차원 공간안에 두 덩어리의 데이터가 있을 것이고,
그 둘을 가르는 초평면(hyperplane)을 찾는 문제가 될 것이다.
초평면에 해당하는 파라미터들은 원래 문제에서 $ \omega $이다.
$ \omega $를 찾는 것이 hyperplane을 찾는 것이다.
$ w^{T}x=0$ 은 decision boundary.
inner product이므로
이 boundary와 $ \omega $는 항상 수직(orthogonal)이다.
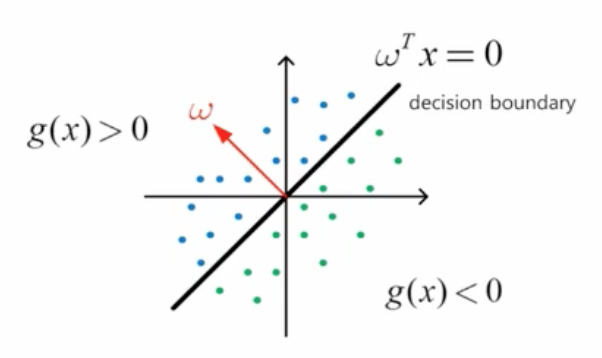
D 공간 상의 데이터가 있다.
결정경계(decision boundary)는 d-1 차원의 hyperplane이 되는 것이다.
'머신러닝과 딥러닝' 카테고리의 다른 글
| 퍼셉트론(Perceptron) (3) (0) | 2020.01.06 |
|---|---|
| 퍼셉트론(Perceptron) (2) (0) | 2020.01.04 |
| 로지스틱 리그레션(Logistic Regression) (0) | 2020.01.02 |
| 최소자승법과 직교투영 (0) | 2019.12.31 |
| 다원 일차 연립방정식 (0) | 2019.12.31 |