데이터 분석에서 왜도와 첨도는 중요한 요소.
왜도
왜도(Skewness)는 데이터의 분포가 한쪽으로 쏠린 것을 의미한다.
Positive Skewness는 왼쪽에 데이터가 많은 형태이다.
Negative Skewness는 오른쪽에 데이터가 많은 형태이다.
Positive Skewness의 예는 아래와 같다.
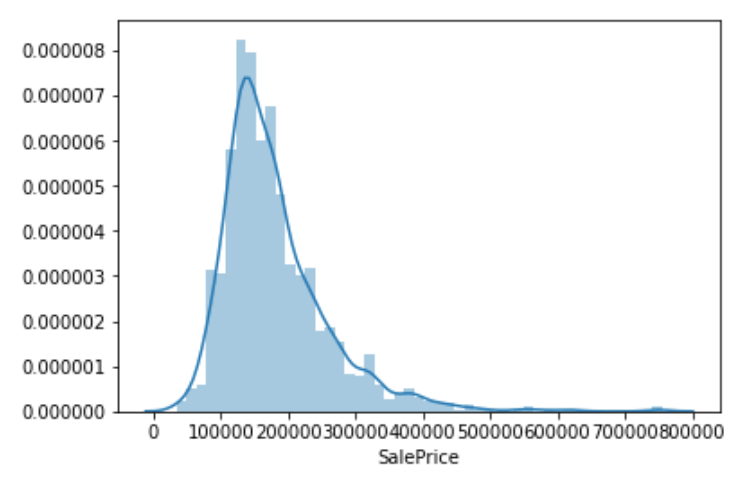
일반적으로 Skewness값이 -2 ~ +2는 치우침이 없는 데이터라고 볼 수 있다.
Skewed 데이터를 변환하는 이유
꼬리에 있는 값을 모델에 제대로 학습시키기 위함
Skewed 되어있는 값을 그대로 학습시키면 꼬리 부분이 상대적으로 모델에 영향이 거의 없이 학습된다.
꼬리 부분이 노이즈가 아니고 유의미한 데이터면 꼬리 부분에 대한 데이터는 예측력이 낮아진다.(학습이 잘 되지 않아서)
변환을 하면, 데이터의 중간값과 꼬리와 가까워져서 모델에 보다 크게 된다.
Skew 데이터를 변환하는 방법은 Square root, cube root, log, outlier 제거 등이 있다.
Positive skewed 변환방법 : square root, cube root, log (밑이 10인 상용로그 )
Negative skewed 변환방법 : square root, cube root, logarithmic (밑이 2인 로그)
첨도
첨도는 분포의 뾰족함이나 평평함에 관련된 것이 아님.
분포의 꼬리에 대한 모든 것이라고 할 수 있음.
한쪽 꼬리 부분의 극값과 다른쪽 꼬리의 극 값 간의 차이를 보여준다. 아웃라이어 찾을 때 사용된다.
첨도가 높으면(Kurtosis > 3) 아웃 라이어가 많이 있다.
첨도가 낮으면(Kurtosis < 3) 극값이 정규분포의 값보다 작기 때문에 결과에 대한 확인이 필요.
+ 정규분포의 첨도는 0이다(기본적 정의에 의하면 3이지만, 일반적으로 정규분포의 첨도를 0으로 만들기 위해 3을 빼서 정의하는 경우가 많다.)
첨도가 0보다 크면 정규분포보다 긴 꼬리를 갖고, 분포가 보다 중앙부분에 덜 집중되어 뾰족한 모양을 가지게 된다.
첨도가 0보다 작으면 정규분포보다 짧은 꼬리를 갖고 분포가 중앙부분에 더 집중되어 중앙부분이 보다 완만한 모양을 가지게 된다.
그래프를 보면서 분포들 간의 뾰족한 정도를 비교할 때 중요한 점
동일한 분산을 가지게 세팅을 하고 비교해야한다.
첨도가 더 큰 분포라 할지라도 분산에 따라 완만한 그래프로 나타날 수 있기 때문임.
https://rucrazia.tistory.com/65
Skewness(왜도)와 Kurtosis(첨도)
데이터 분석에서 Skewness(왜도)와 Kurtosis(첨도)는 중요한 요소이다. 데이터의 분포가 한쪽으로 쏠린 것을 의미하는 Skewness는 positive Skewness와 Negative Skewness로 나뉜다. Positive Skewness는 오른쪽에..
rucrazia.tistory.com
'기초통계' 카테고리의 다른 글
| 베이즈 이론(Bayes Theorem) (0) | 2020.01.24 |
|---|---|
| 주변확률분포와 기댓값, 분산, 공분산, 상관계수 (0) | 2019.12.16 |
| 이산확률변수의 결합확률분포 (0) | 2019.12.12 |
| 확률질량함수 (0) | 2019.12.12 |
| 확률(Probability) vs 가능도(Likelihood) (0) | 2019.12.12 |