가장 쉬운 문제
제약 조건이 없는 1차원 문제

objective function이 위와 같이 생겼으면
$ x^{*} $ 를 어떻게 찾을 것 인가?
$ f(x)$가 정의된다면 $ f'(x)=0$을 찾으면 된다.
기울기가 0이 되게하는 $ x^{*} $가 최적해가 된다는 것을 알고 있다.
그래디언트는 n차원 벡터인데
n차원 벡터에 대해서 다 편미분하는것.
n개의 컴포넌트를 칼럼 벡터 요소로 가지는 것을 그래디언트로 정의한다.
모든 축 방향으로 기울기 계산을 하고 최적해의 솔루션은 역시나 제약이 없을 경우에 아래의 조건을 만족한다.
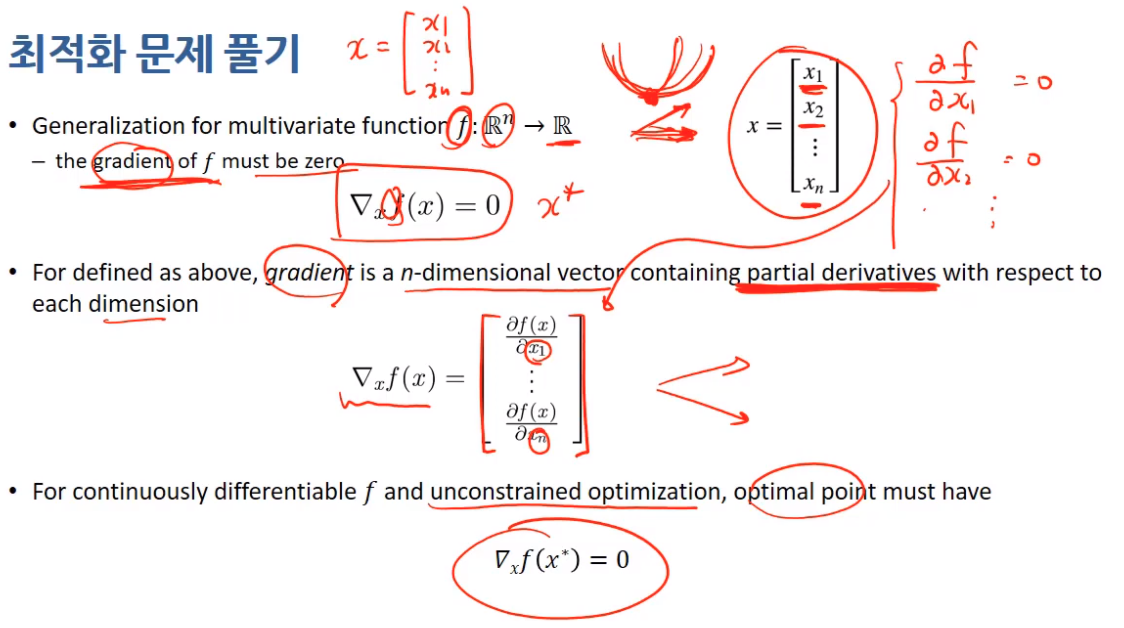
아래와 같이 $f(x)$가 있을 때 최적해 구하면... 다음과 같다.
$ x_{1} $ 에 대해서 미분
$ x_{2} $ 에 대해서 미분

그래디언트, 구배 ?
1D -> N차원 확장
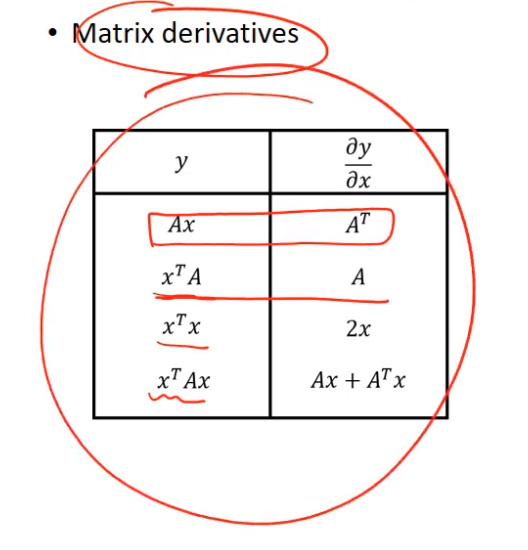
행렬 미분하는 경우...표를 참조하길 바람. 외우지말고!
행렬의 형태로 다시 풀어보면 다음과 같다.

https://www.youtube.com/watch?v=OJ397Y3fVkY
'머신러닝과 딥러닝' 카테고리의 다른 글
| CVXPY를 사용한 최적화 문제 풀기 (2) (0) | 2019.12.31 |
|---|---|
| CVXPY를 사용한 최적화 문제 풀기 (1) (0) | 2019.12.30 |
| 최적화와 볼록최적화(Optimization and Convex Optimization) (0) | 2019.12.30 |
| 벡터의 크기와 직교성 (0) | 2019.12.30 |
| 선형변환과 행렬 (0) | 2019.12.30 |