최단거리 문제 1

파란색 공간에서 [3,3]까지 가장 가까운 자리가 어디인가? 직관적으로 [1.5, 1.5]이지만...
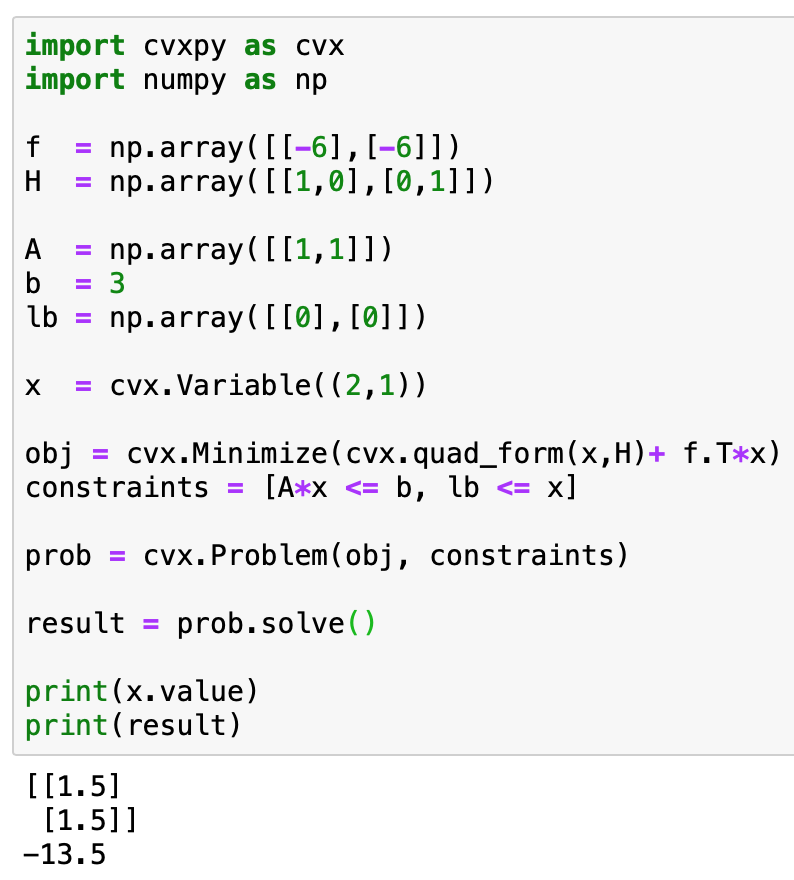
이러한 문제를 fomulation을 하고 cvx로 풀어보는 것이 의미가 있다.
결정변수를 $ x_{1}, x_{2} $ 로 하고...
직선의 최단거리를 아래와 같이 표현할 수 있다.
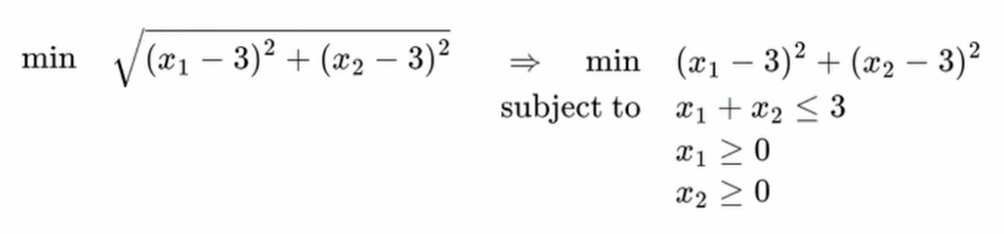
최소화 하겠다.
제약조건도 함께 생각해보자.
루트가 씌워져 있다.
최적화 문제에서 잘 생각해보면 전체에 제곱을 해도 목적함수의 값은 변경되겠지만 최적해는 변하지 않는다.

최단거리 문제 2
$ \vec {a} $ 에서 출발해서
바다에 가서 물을 담아서 $ \vec {b} $로 가야하는 문제?
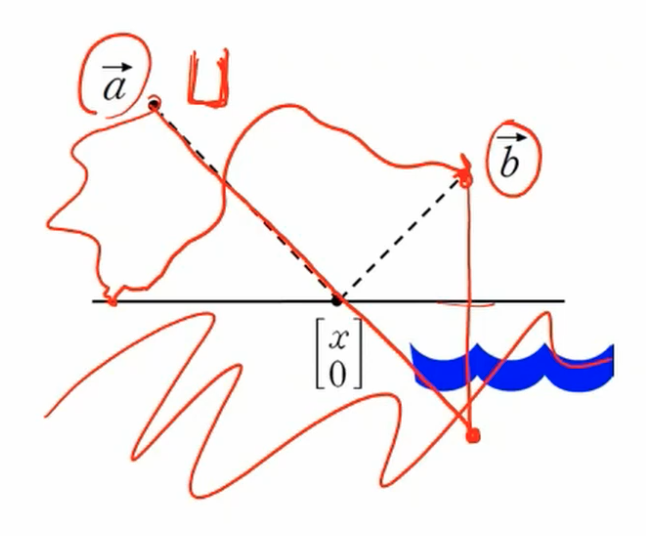
($x$와 $\vec {a}$ 사이의 거리) + ($x$와 $\vec {b}$ 사이의 거리) <--- 최소화하자!
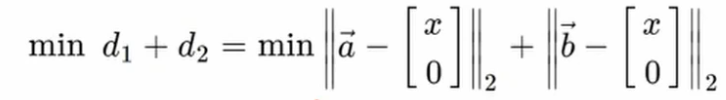
조금 더 생각해보면...
물이 없으면 가볍고, 물이 있으면 무겁다.
$ d_{2} $는 훨씬 무겁다. $ \mu $라는 것을 포함시킨다. 좀더 실질적이다.

물이 많이 무겁다면...물 뜨기 전에 위치 b쪽으로 더 가깝게 걷게 될 수 있음.
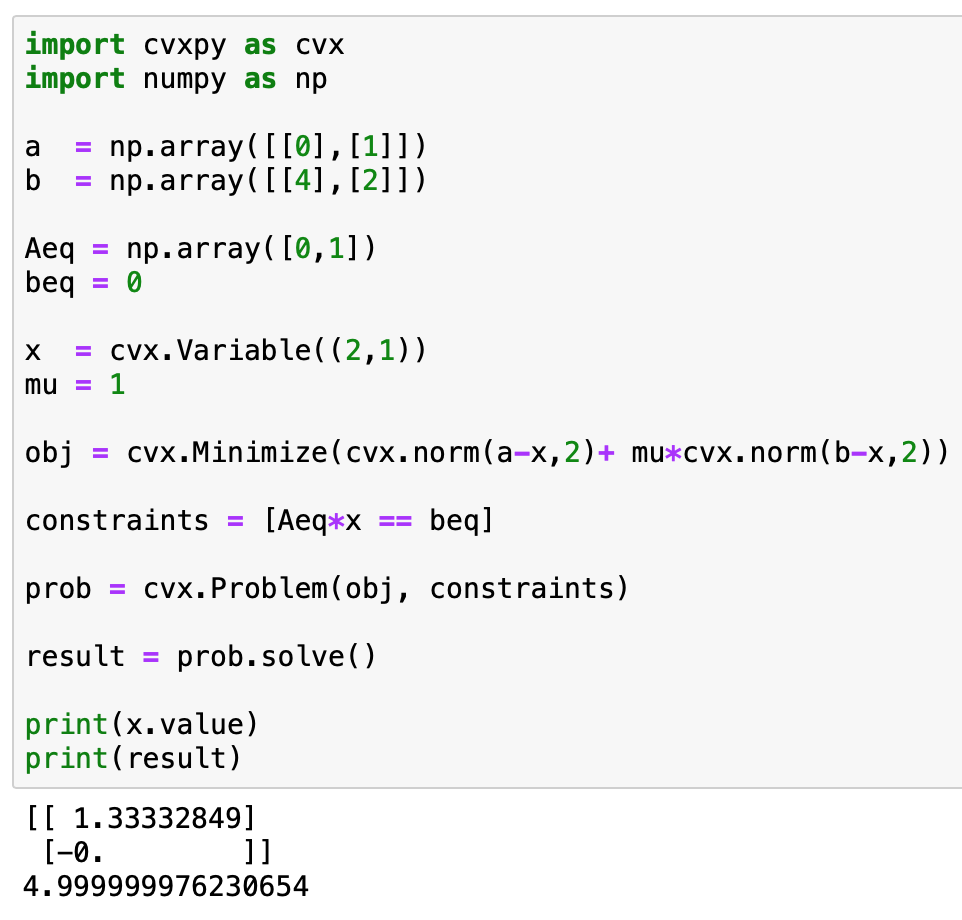
1.33 쯤에 위치한다.
물류 문제
최적화 하는 포인트를 찾아라. 매우 간단한 문제임.
물건을 이송해야하는데, 배달해야는 위치가 A가 있고 B가 있고 C가 있다.
수송비용이라 생각해도 되고 거리로 생각해도 된다.
어느 곳에 입지해야 물류 비용을 최소화 할 수 있는가?
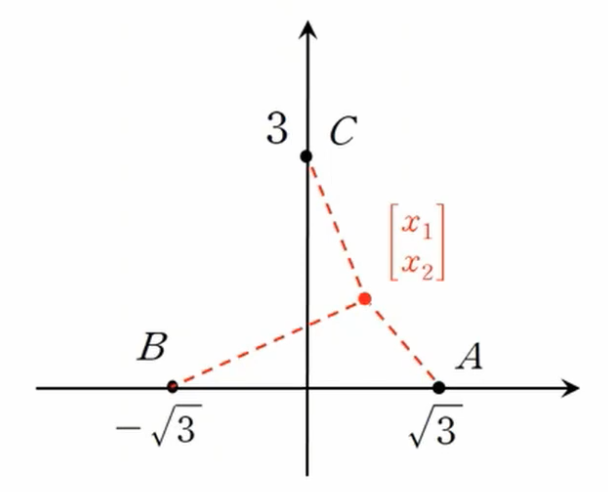
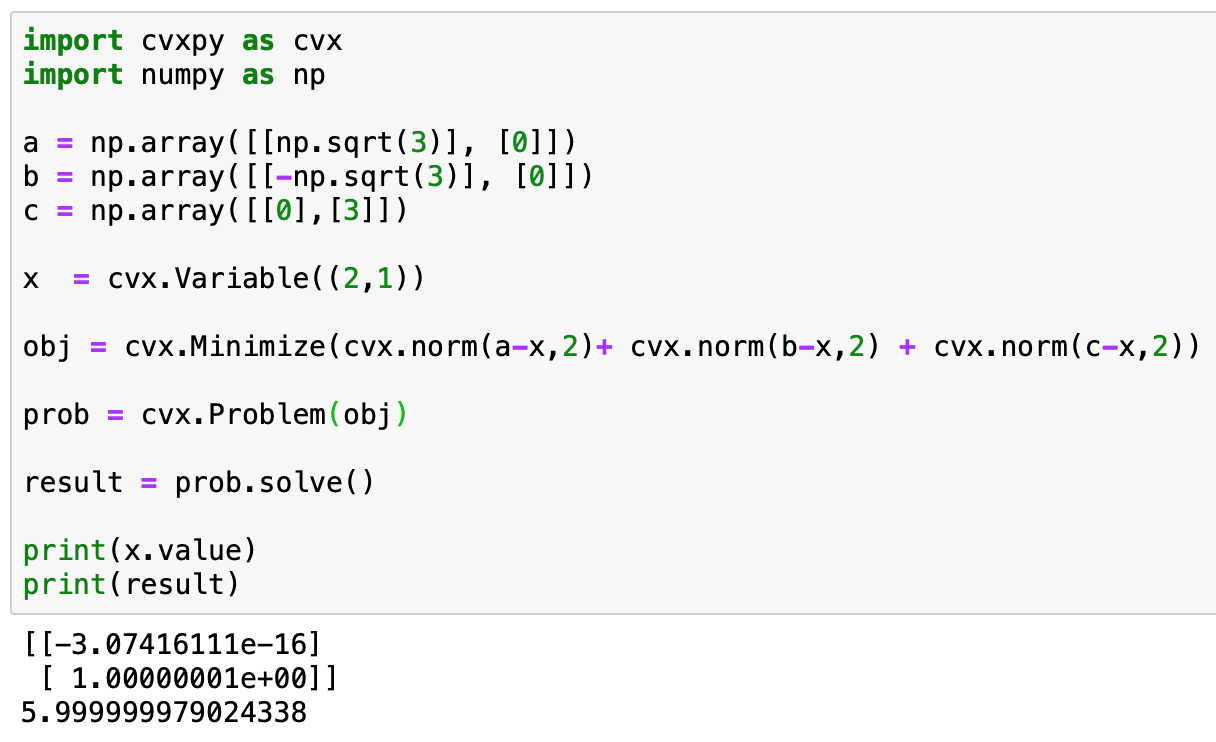
[0,1]이라는 것을 알 수 있다.
'머신러닝과 딥러닝' 카테고리의 다른 글
| 최소자승법과 직교투영 (0) | 2019.12.31 |
|---|---|
| 다원 일차 연립방정식 (0) | 2019.12.31 |
| CVXPY를 사용한 최적화 문제 풀기 (1) (0) | 2019.12.30 |
| 최적화 문제 풀기 (0) | 2019.12.30 |
| 최적화와 볼록최적화(Optimization and Convex Optimization) (0) | 2019.12.30 |